BeerBellyBlunt

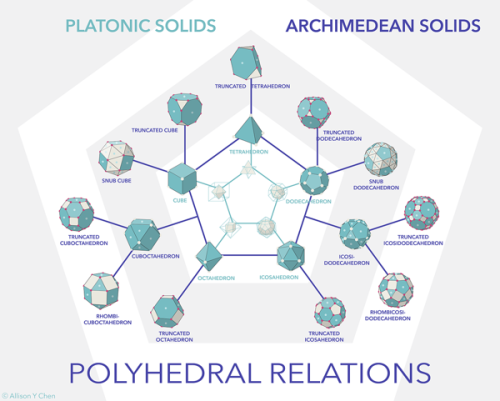
Platonic solid: In Euclidean geometry, a Platonic solid is a regular, convex polyhedron with congruent faces of regular polygons and the same number of faces meeting at each vertex. Five solids meet those criteria, and each is named after its number of faces.

An Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices . They are distinct from the Platonic soilds, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.

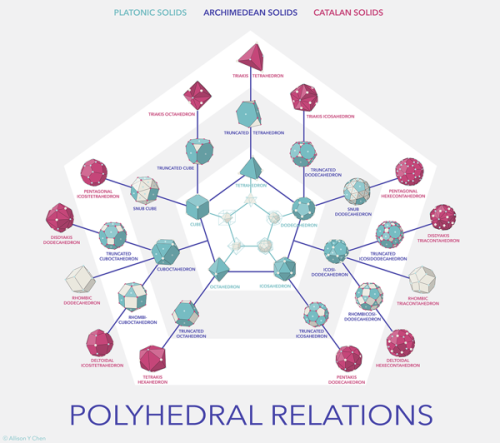
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean soild. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865.

The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic soilds  and Archimedean soild, the faces of Catalan solids are not regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids.

Images: Polyhedral Relations by Allison Chen on Behance.

Can you flatten a sphere?

The answer is NO, you can not. This is why all map projections are innacurate and distorted, requiring some form of compromise between how accurate the angles, distances and areas in a globe are represented.

This is all due to Gauss’s Theorema Egregium, which dictates that you can only bend surfaces without distortion/stretching if you don’t change their Gaussian curvature.

The Gaussian curvature is an intrinsic and important property of a surface. Planes, cylinders and cones all have zero Gaussian curvature, and this is why you can make a tube or a party hat out of a flat piece of paper. A sphere has a positive Gaussian curvature, and a saddle shape has a negative one, so you cannot make those starting out with something flat.

If you like pizza then you are probably intimately familiar with this theorem. That universal trick of bending a pizza slice so it stiffens up is a direct result of the theorem, as the bend forces the other direction to stay flat as to maintain zero Gaussian curvature on the slice. Here’s a Numberphile video explaining it in more detail.

However, there are several ways to approximate a sphere as a collection of shapes you can flatten. For instance, you can project the surface of the sphere onto an icosahedron, a solid with 20 equal triangular faces, giving you what it is called the Dymaxion projection.

The Dymaxion map projection.

The problem with this technique is that you still have a sphere approximated by flat shapes, and not curved ones.

One of the earliest proofs of the surface area of the sphere (4πr2) came from the great Greek mathematician Archimedes. He realized that he could approximate the surface of the sphere arbitrarily close by stacks of truncated cones. The animation below shows this construction.

The great thing about cones is that not only they are curved surfaces, they also have zero curvature! This means we can flatten each of those conical strips onto a flat sheet of paper, which will then be a good approximation of a sphere.

So what does this flattened sphere approximated by conical strips look like? Check the image below.

But this is not the only way to distribute the strips. We could also align them by a corner, like this:

All of this is not exactly new, of course, but I never saw anyone assembling one of these. I wanted to try it out with paper, and that photo above is the result.

It’s really hard to put together and it doesn’t hold itself up too well, but it’s a nice little reminder that math works after all!

Here’s the PDF to print it out, if you want to try it yourself. Send me a picture if you do!

The best vintage cars, hot rods, and kustoms

{ insp. }

Modified Stems: Thorn

Thorns are modified branches or stems. Thorns and spines are derived from shoots and leaves respectively, and have vascular bundles inside, whereas prickles (like rose prickles) do not have vascular bundles inside. The tree shown in the picture above is called the honey locust tree, also known as the thorny locust. Just look at those thorns!

Modified Stems Part:   1     2     3     4     5     6

Ferns

Ferns are more advanced primitive vascular plants. They have true roots, stems, and leaves. Ferns do not have seeds, but produce spores instead. Fern’s lifecycle, unlike primitive non-vascular plants such as bryophytes, is dominated by the sporophyte generation. Some interesting terminology associated with ferns are frond, pinnae, sori, rhizome, and fiddlehead. A frond describes the entire blade of the fern and the smaller individual leaflets are called pinnae. Sori describes clusters of sporangia on the underside of the pinnae (Sori are depicted in the second photo). A rhizome is an underground stem that puts out shoots and adventitious roots. Fiddleheads are furled fronds of a young fern.

Click for more vintage cars, hot rods, and kustoms

“In 1972, Edward Lorenz gave a presentation titled: “Predictability: Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?” The term “butterfly effect” was born. Lorenz, who was born on this day in 1917, was a pioneer of chaos theory, which analyzes how subtle changes in the initial conditions of a system can lead to widely differing outcomes. This 2013 Physics Today article examines Lorenz and the birth of chaos theory.” - Physics Today

Chaos at fifty by Adilson E. Motter and David K. Campbell is an article that lays out the discovery of chaos. I found it a very satisfying and informative read about dynamical systems, the butterfly effect, bifurcations, predictability and fractals. You should probably go check it out by clicking on the bolded title. 👍

“Chaos sets itself apart from other great revolutions in the physical sciences. In contrast to, say, relativity or quantum mechanics, chaos is not a theory of any particular physical phenomenon. Rather, it is a paradigm shift of all science, which provides a collection of concepts and methods to analyze a novel behavior that can arise in a wide range of disciplines.” - Chaos at fifty

Image above: “The Lorenz attractor, as revealed by the never-repeating trajectory of a single chaotic orbit. The spheres shown here represent iterations of the so-called Lorenz equations, calculated using the original parameters in Edward Lorenz’s seminal work. (Spheres are colored according to the iteration count.) From certain angles, the two lobes of the attractor resemble a butterfly, a coincidence that helped earn sensitive dependence on initial conditions its nickname—the butterfly effect. An animated visualization of the attractor is available here. (Image courtesy of Stefan Ganev.)”

↙↙↙