Modified Stems: Thorn

The best vintage cars, hot rods, and kustoms

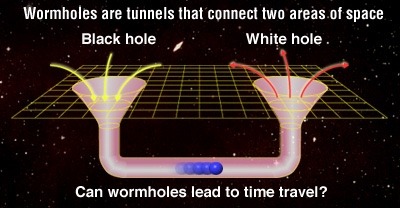
Wormholes

Also known as Einstein-Rosen Bridges are theoretically possible going by Einstein’s theory, and equations of general relativity. Basically wormholes take advantage of our 3 dimensional space and are able to “bend” it. Picture a sheet of paper; now put two circular holes on each end of that sheet of paper. Normally the quickest way to join one point to the other would be to draw a straight line between them. Now instead, you could fold the piece of paper so each hole is touching meaning that there is no longer any distance between them. This is an analogy of how a wormhole works except instead of a circular hole on a 2D plane, the entry and exit points of an Einstein-Rosen bridge can be visualised as spheres in a 3D space.

While the theory of general relativity allows the existence of wormholes, we have not yet found physical evidence. The first wormhole solution discovered was the Schwarzschild wormhole presented in the Schwarzschild metric describing an eternal black hole. However this is not stable enough and would collapse before anything could cross from one end to the other. Traversable wormholes could exist of there was a form of exotic matter with a negative energy to stabilise them.

The Casmir effect shows that quantum field theory allows the energy density in some space to be relatively lower than the ordinary vacuum of space. A lot of physicists (like Stephen Hawking) use this to argue that it is possible to stabilise a traversable wormhole. However there are no known natural processes that would cause a traversable wormhole to stabilise.

The quantum foam hypothesis can be used to suggest the spontaneous appearance of tiny black holes at the Planck scale. Stable versions of these tiny wormholes have been suggested as dark matter candidates. It is also possible that one of these wormholes opened into a previously empty space from another universe, held open by a cosmic string (1D string) with a negative mass then it could be inflated to a macroscopic size by cosmic inflation. Is it possible this happened at the start of the Big Bang?

Ferns

Ferns are more advanced primitive vascular plants. They have true roots, stems, and leaves. Ferns do not have seeds, but produce spores instead. Fern’s lifecycle, unlike primitive non-vascular plants such as bryophytes, is dominated by the sporophyte generation. Some interesting terminology associated with ferns are frond, pinnae, sori, rhizome, and fiddlehead. A frond describes the entire blade of the fern and the smaller individual leaflets are called pinnae. Sori describes clusters of sporangia on the underside of the pinnae (Sori are depicted in the second photo). A rhizome is an underground stem that puts out shoots and adventitious roots. Fiddleheads are furled fronds of a young fern.

“I do not sleep well. My mind will not let me. It is going night and day. There is no more tyrannical thing than a mind that is accustomed to thought. It really seems to resent me falling asleep. It pounds for attention until I wake up again.“

–Nikola Tesla

“Tesla Predicts New Source of Power In Year.” New York Herald Tribune. July 9, 1933.

Scientists have created a fluid with negative mass – but what does it tell us?

The fluid, which defies everyday laws of motion, is a rare achievement and provides a platform to study an otherwise hypothetical form of matter

Scientists have created a fluid that exhibits the bizarre property of “negative mass” in an experiment that appears to defy the everyday laws of motion.

Push an object and Newton’s laws (and common experience) dictate that it will accelerate in the direction in which it was shoved.

“That’s what most things that we’re used to do,” said Matthew Forbes, a physicist at Washington State University and co-author of the paper, which shows that normal intuitions do not always apply to physics experiments. “With negative mass, if you push something, it accelerates toward you.”

Negative mass has previously cropped up in speculative theories, including those suggesting the existence of wormholes, a form of cosmological shortcut between two points in the universe. Just as electric charge can be either positive or negative, matter could, hypothetically, have either positive or negative mass.

For an object with negative mass, Newton’s second law of motion, in which a force is equal to the mass of an object multiplied by its acceleration (F=ma) would be experienced in reverse.

Continue Reading.

Can you flatten a sphere?

The answer is NO, you can not. This is why all map projections are innacurate and distorted, requiring some form of compromise between how accurate the angles, distances and areas in a globe are represented.

This is all due to Gauss’s Theorema Egregium, which dictates that you can only bend surfaces without distortion/stretching if you don’t change their Gaussian curvature.

The Gaussian curvature is an intrinsic and important property of a surface. Planes, cylinders and cones all have zero Gaussian curvature, and this is why you can make a tube or a party hat out of a flat piece of paper. A sphere has a positive Gaussian curvature, and a saddle shape has a negative one, so you cannot make those starting out with something flat.

If you like pizza then you are probably intimately familiar with this theorem. That universal trick of bending a pizza slice so it stiffens up is a direct result of the theorem, as the bend forces the other direction to stay flat as to maintain zero Gaussian curvature on the slice. Here’s a Numberphile video explaining it in more detail.

However, there are several ways to approximate a sphere as a collection of shapes you can flatten. For instance, you can project the surface of the sphere onto an icosahedron, a solid with 20 equal triangular faces, giving you what it is called the Dymaxion projection.

The Dymaxion map projection.

The problem with this technique is that you still have a sphere approximated by flat shapes, and not curved ones.

One of the earliest proofs of the surface area of the sphere (4πr2) came from the great Greek mathematician Archimedes. He realized that he could approximate the surface of the sphere arbitrarily close by stacks of truncated cones. The animation below shows this construction.

The great thing about cones is that not only they are curved surfaces, they also have zero curvature! This means we can flatten each of those conical strips onto a flat sheet of paper, which will then be a good approximation of a sphere.

So what does this flattened sphere approximated by conical strips look like? Check the image below.

But this is not the only way to distribute the strips. We could also align them by a corner, like this:

All of this is not exactly new, of course, but I never saw anyone assembling one of these. I wanted to try it out with paper, and that photo above is the result.

It’s really hard to put together and it doesn’t hold itself up too well, but it’s a nice little reminder that math works after all!

Here’s the PDF to print it out, if you want to try it yourself. Send me a picture if you do!