Can You Flatten A Sphere?

The Worlds of our Solar System

Science, my lad, is made up of mistakes, but they are mistakes which it is useful to make, because they lead little by little to the truth.

Jules Verne , Journey to the Center of the Earth (via q-lvck)

I guess it’s also the right setting for pictures of the Moon at night.

ISS Solar Transit [Explained]

“In 1972, Edward Lorenz gave a presentation titled: “Predictability: Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?” The term “butterfly effect” was born. Lorenz, who was born on this day in 1917, was a pioneer of chaos theory, which analyzes how subtle changes in the initial conditions of a system can lead to widely differing outcomes. This 2013 Physics Today article examines Lorenz and the birth of chaos theory.” - Physics Today

Chaos at fifty by Adilson E. Motter and David K. Campbell is an article that lays out the discovery of chaos. I found it a very satisfying and informative read about dynamical systems, the butterfly effect, bifurcations, predictability and fractals. You should probably go check it out by clicking on the bolded title. 👍

“Chaos sets itself apart from other great revolutions in the physical sciences. In contrast to, say, relativity or quantum mechanics, chaos is not a theory of any particular physical phenomenon. Rather, it is a paradigm shift of all science, which provides a collection of concepts and methods to analyze a novel behavior that can arise in a wide range of disciplines.” - Chaos at fifty

Image above: “The Lorenz attractor, as revealed by the never-repeating trajectory of a single chaotic orbit. The spheres shown here represent iterations of the so-called Lorenz equations, calculated using the original parameters in Edward Lorenz’s seminal work. (Spheres are colored according to the iteration count.) From certain angles, the two lobes of the attractor resemble a butterfly, a coincidence that helped earn sensitive dependence on initial conditions its nickname—the butterfly effect. An animated visualization of the attractor is available here. (Image courtesy of Stefan Ganev.)”

😂😂

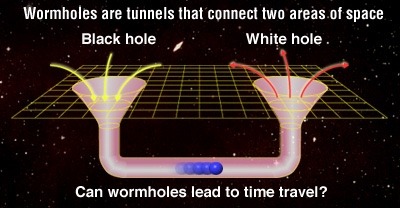
Wormholes

Also known as Einstein-Rosen Bridges are theoretically possible going by Einstein’s theory, and equations of general relativity. Basically wormholes take advantage of our 3 dimensional space and are able to “bend” it. Picture a sheet of paper; now put two circular holes on each end of that sheet of paper. Normally the quickest way to join one point to the other would be to draw a straight line between them. Now instead, you could fold the piece of paper so each hole is touching meaning that there is no longer any distance between them. This is an analogy of how a wormhole works except instead of a circular hole on a 2D plane, the entry and exit points of an Einstein-Rosen bridge can be visualised as spheres in a 3D space.

While the theory of general relativity allows the existence of wormholes, we have not yet found physical evidence. The first wormhole solution discovered was the Schwarzschild wormhole presented in the Schwarzschild metric describing an eternal black hole. However this is not stable enough and would collapse before anything could cross from one end to the other. Traversable wormholes could exist of there was a form of exotic matter with a negative energy to stabilise them.

The Casmir effect shows that quantum field theory allows the energy density in some space to be relatively lower than the ordinary vacuum of space. A lot of physicists (like Stephen Hawking) use this to argue that it is possible to stabilise a traversable wormhole. However there are no known natural processes that would cause a traversable wormhole to stabilise.

The quantum foam hypothesis can be used to suggest the spontaneous appearance of tiny black holes at the Planck scale. Stable versions of these tiny wormholes have been suggested as dark matter candidates. It is also possible that one of these wormholes opened into a previously empty space from another universe, held open by a cosmic string (1D string) with a negative mass then it could be inflated to a macroscopic size by cosmic inflation. Is it possible this happened at the start of the Big Bang?

Fairlytale Scandinavian Green Roofs

Scandinavians are serious about their green roofs. They’ve had them for a while now and it doesn’t look like they’re going anywhere. They even have a competition every year to determine the best green roof project in Scandinavia by the Scandinavian Green Roof Association! But there is a reason why Scandinavians like these green roofs so much… They are not only a beautiful feature for a house, but they also offer numerous social, environmental and financial benefits. They absorb rainwater, reduce winter heating costs, reduce summer air-conditioning costs, provide insulation, and are long lasting - just to name a few.

Images and text via

😊

Alloys: Bronze

Given that there are many different types of bronze with a wide variety of elements included, the alloy cannot be defined as having one set composition. Though the most well known bronze is likely the common copper-tin alloy, alloys such as bismuth bronze, silicon bronze, and aluminum bronze don’t necessarily contain tin.

That being said, the most well known bronze alloy, and the one most people probably think of when they hear the word, is composed of mostly copper with tin or arsenic and, potentially, small amounts of other elements. The oldest tin-copper bronze alloys found are from around 4500 B.C., and this replacement of stone tools with bronze eventually led to the Bronze Age. (The Bronze Age eventually gave way to the Iron Age, because, despite bronze’s favorable properties, iron is more plentiful and easier to find.)

The addition of tin, arsenic, and other elements produces a harder material than copper alone. Bronze also has the favorable properties of being corrosion resistant, non-magnetic, has excellent heat transfer properties, is relatively easy to machine, withstands high temperatures, and is resistant to wear and friction. Unlike steel, bronze does not spark when struck and is therefore useful as tools in environments containing flammable vapors. 

Some historical applications of bronze include in statues, weapons and tools, and currency/coinage. The alloys is also well known for is usage in musical instruments, often bells and cymbals, as well as the windings of string instruments such as the guitar and piano. 

Sources: ( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 5 )

Image sources: ( 1 ) ( 2 ) ( 3 )