Sleepysneezeydopeydoc-blog - Physics Nerd

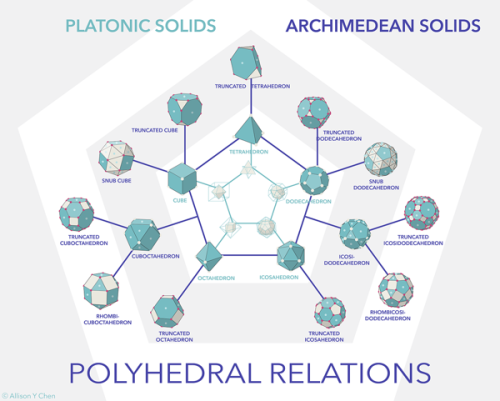
Platonic solid: In Euclidean geometry, a Platonic solid is a regular, convex polyhedron with congruent faces of regular polygons and the same number of faces meeting at each vertex. Five solids meet those criteria, and each is named after its number of faces.

An Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices . They are distinct from the Platonic soilds, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.

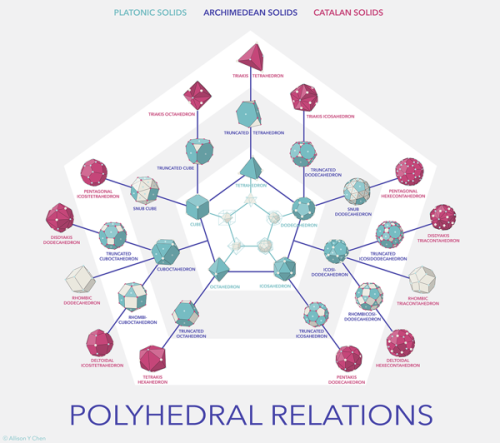
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean soild. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865.

The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic soilds  and Archimedean soild, the faces of Catalan solids are not regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids.

Images: Polyhedral Relations by Allison Chen on Behance.

Short version of the Higgs boson and Higgs field

The Higgs boson is the theoretical particle that gives rise to the mass of fundamental particles. It does this as a field that spans across the whole of the universe and you can think of it as someone trying to walk from one side of the room but they are up to their knees in water. The more drag the particle has in the field hence the slower it moves, the more mass it has. One thing to bear in mind is that this does not explain the mass created through quark confinement which is where most of our mass comes from.

The Higgs boson is predicted to have a mass of about 125GeV and would have a spin of 0 which is what makes it a boson.

Now, we know that mass and energy are interchangeable terms, photons have 0 mass and so one would expect then to have 0 energy, but E=had allows a photon to have energy but only when it is travelling at the speed of light.

Now this has been very brief and simple and not incredibly accurate, I hope this helps some of you understand the Higgs Boson.

Click for more vintage cars, hot rods, and kustoms

Modified Leaves: Insect Traps

Carnivorous plants are plants that derive some or most of their nutrients (not energy) from trapping and consuming animals, typically insects. Carnivorous plants have adapted to grow in places where the soil is thin or poor in nutrients, especially nitrogen, such as acidic bogs and rock outcroppings. These carnivorous plants have modified leaves that help to trap and digest prey.

The carnivorous plant in the first picture is a Venus flytrap that belongs to the genus Dionaea. The Venus flytrap has small trigger hairs on the inside of its leaf that cause the trap to close around its prey. The carnivorous plant in the middle picture is a sundew that belongs to the Drosera. Sundews have small tentacles, topped with sticky secretions, that cover the leaves.  Sundews are able to move their tentacles towards the center of the leaf to bring the insect into contact with as many stalked glands as possible. The carnivorous plant in the bottom picture is a  species of North American pitcher plants that are commonly called trumpet pitchers. Insects fall into the pitcher plant and cannot climb out. Meanwhile, digestive enzymes in the pitcher leaf break down the prey.

Modified Leaves Part:   1    2     3     4     5     6

Can you flatten a sphere?

The answer is NO, you can not. This is why all map projections are innacurate and distorted, requiring some form of compromise between how accurate the angles, distances and areas in a globe are represented.

This is all due to Gauss’s Theorema Egregium, which dictates that you can only bend surfaces without distortion/stretching if you don’t change their Gaussian curvature.

The Gaussian curvature is an intrinsic and important property of a surface. Planes, cylinders and cones all have zero Gaussian curvature, and this is why you can make a tube or a party hat out of a flat piece of paper. A sphere has a positive Gaussian curvature, and a saddle shape has a negative one, so you cannot make those starting out with something flat.

If you like pizza then you are probably intimately familiar with this theorem. That universal trick of bending a pizza slice so it stiffens up is a direct result of the theorem, as the bend forces the other direction to stay flat as to maintain zero Gaussian curvature on the slice. Here’s a Numberphile video explaining it in more detail.

However, there are several ways to approximate a sphere as a collection of shapes you can flatten. For instance, you can project the surface of the sphere onto an icosahedron, a solid with 20 equal triangular faces, giving you what it is called the Dymaxion projection.

The Dymaxion map projection.

The problem with this technique is that you still have a sphere approximated by flat shapes, and not curved ones.

One of the earliest proofs of the surface area of the sphere (4πr2) came from the great Greek mathematician Archimedes. He realized that he could approximate the surface of the sphere arbitrarily close by stacks of truncated cones. The animation below shows this construction.

The great thing about cones is that not only they are curved surfaces, they also have zero curvature! This means we can flatten each of those conical strips onto a flat sheet of paper, which will then be a good approximation of a sphere.

So what does this flattened sphere approximated by conical strips look like? Check the image below.

But this is not the only way to distribute the strips. We could also align them by a corner, like this:

All of this is not exactly new, of course, but I never saw anyone assembling one of these. I wanted to try it out with paper, and that photo above is the result.

It’s really hard to put together and it doesn’t hold itself up too well, but it’s a nice little reminder that math works after all!

Here’s the PDF to print it out, if you want to try it yourself. Send me a picture if you do!

On the care and keeping of your scientist

Congratulations on adopting a scientist! Regardless of their field they will require much coffee, free food, and love. Here are some field specific tips for keeping your scientist happy and healthy!

Biology: make sure they don't get overly invested in their model organism by reminding them about the flaws inherent in their system on a regular basis, but also make sure to join in when they criticize other models in favor of their own

Chemistry: don't let them do that 'just one more reaction' at 10 pm. make sure they get out of the lab and see the sun on a regular basis. try to keep them from partying too hard when they do leave the lab

Geology: humor their rock puns but don't let the lick the rocks (they will tell you they need to lick the rocks to identify them, but don't fall for it)

Astronomy: try not to let them become completely nocturnal. point out nice stars to them and look suitably impressed by their "pictures" of planets that don't look like anything to you

Physics: take them to the park on a regular basis to remind them that things larger than subatomic particles exist. bring a frisbee or a ball to play catch with and be impressed by their ability to calculate trajectories

Math: always make sure to have free batteries for their calculators and a mathmatica user guide on hand. Humor them when they tell you why space without angles is important

Ecology: make sure they remember to wear sunscreen and keep an eye on them in the field. Remind them to come inside and analyze their data occasionally

Psychology: don't mention Freud or ever call them a soft or social science, but make sure you gently remind them that social factors can impact reproducibility and try to keep them from drawing sweeping conclusions about the inherent nature of humanity

Neuroscience: be suitably impressed by their newest experiment and then remind them that people are not mice as often as possible

Computer Science: make sure they take breaks while debugging by limiting their supply of coffee. Nod and smile when they go off on indexing and arrays. Make sure they always have a rubber duck.

Make sure to keep your scientist away from engineers unless they have been properly socialized to interact in a translational household. The most important thing is to remember to hug your scientist on a regular basis and remind them that there is life outside the lab

Happy national periodic table day!