Sleepysneezeydopeydoc-blog - Physics Nerd

“We TOLD you it was hard.” “Yeah, but now that I’VE tried, we KNOW it’s hard.”

Here to Help [Explained]

Dark Energy

Dark energy is in physical cosmology and astrology as an unknown form of energy that permeates through space making up for 68.3% of the observable universe (dark matter takes up 26.8%, only 4.9% is ordinary matter). Dark energy is currently the most accepted hypothesis to explain why the universe is expanding at an accelerated rate (if the observable universe comprised of only the ordinary matter we see, the universe would be expanding at a much slower rate than it currently is thus meaning dark matter and dark energy make up the mass for the accelerated rate of expansion). On a mass–energy equivalence basis, the density of dark energy (6.91 × 10^−27 kg/m3) is very low, much less than the density of ordinary matter or dark matter within galaxies.

Dark energy is not known to react with any of the fundamental forces other than gravity. It clearly has a large impact on the universe making up for 68.3% of universal density, only because it fills an otherwise empty space. The two current leading models are a cosmological constant and quintessence. Both models conclude that dark energy must have a negative pressure.

The effect of dark energy: a small constant negative pressure of vacuum

An all-time classic to celebrate St. Valentine’s day! 🤗💘

Can you flatten a sphere?

The answer is NO, you can not. This is why all map projections are innacurate and distorted, requiring some form of compromise between how accurate the angles, distances and areas in a globe are represented.

This is all due to Gauss’s Theorema Egregium, which dictates that you can only bend surfaces without distortion/stretching if you don’t change their Gaussian curvature.

The Gaussian curvature is an intrinsic and important property of a surface. Planes, cylinders and cones all have zero Gaussian curvature, and this is why you can make a tube or a party hat out of a flat piece of paper. A sphere has a positive Gaussian curvature, and a saddle shape has a negative one, so you cannot make those starting out with something flat.

If you like pizza then you are probably intimately familiar with this theorem. That universal trick of bending a pizza slice so it stiffens up is a direct result of the theorem, as the bend forces the other direction to stay flat as to maintain zero Gaussian curvature on the slice. Here’s a Numberphile video explaining it in more detail.

However, there are several ways to approximate a sphere as a collection of shapes you can flatten. For instance, you can project the surface of the sphere onto an icosahedron, a solid with 20 equal triangular faces, giving you what it is called the Dymaxion projection.

The Dymaxion map projection.

The problem with this technique is that you still have a sphere approximated by flat shapes, and not curved ones.

One of the earliest proofs of the surface area of the sphere (4πr2) came from the great Greek mathematician Archimedes. He realized that he could approximate the surface of the sphere arbitrarily close by stacks of truncated cones. The animation below shows this construction.

The great thing about cones is that not only they are curved surfaces, they also have zero curvature! This means we can flatten each of those conical strips onto a flat sheet of paper, which will then be a good approximation of a sphere.

So what does this flattened sphere approximated by conical strips look like? Check the image below.

But this is not the only way to distribute the strips. We could also align them by a corner, like this:

All of this is not exactly new, of course, but I never saw anyone assembling one of these. I wanted to try it out with paper, and that photo above is the result.

It’s really hard to put together and it doesn’t hold itself up too well, but it’s a nice little reminder that math works after all!

Here’s the PDF to print it out, if you want to try it yourself. Send me a picture if you do!

Old but gold 💛

I guess it’s also the right setting for pictures of the Moon at night.

ISS Solar Transit [Explained]

Ratrod Moskvich IZH 2715 pickup from Fast Family Show (Moscow, 2017)

Via 

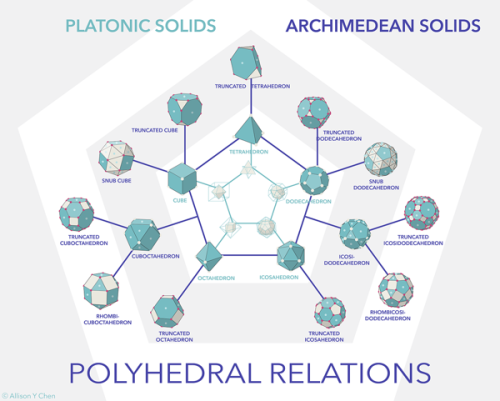
Platonic solid: In Euclidean geometry, a Platonic solid is a regular, convex polyhedron with congruent faces of regular polygons and the same number of faces meeting at each vertex. Five solids meet those criteria, and each is named after its number of faces.

An Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices . They are distinct from the Platonic soilds, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.

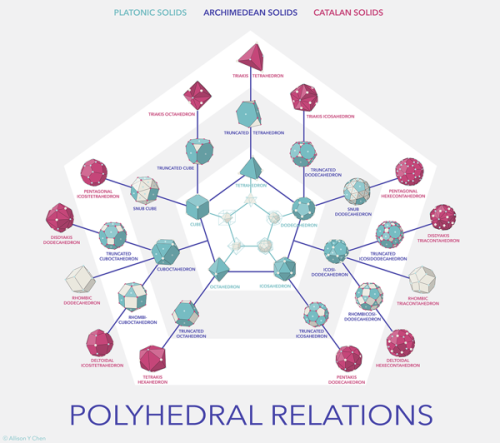
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean soild. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865.

The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic soilds  and Archimedean soild, the faces of Catalan solids are not regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids.

Images: Polyhedral Relations by Allison Chen on Behance.