I Wish I Could Have Been There.

I would not sit there. Who knows how much radiation is there 😨

End to the universe ends your ideas of infinite

If the big rip or vacuum decay takes place then numbers can’t be infinite, infinity to finite

Photography by Juh-ku

🎸🤘

Fairlytale Scandinavian Green Roofs

Scandinavians are serious about their green roofs. They’ve had them for a while now and it doesn’t look like they’re going anywhere. They even have a competition every year to determine the best green roof project in Scandinavia by the Scandinavian Green Roof Association! But there is a reason why Scandinavians like these green roofs so much… They are not only a beautiful feature for a house, but they also offer numerous social, environmental and financial benefits. They absorb rainwater, reduce winter heating costs, reduce summer air-conditioning costs, provide insulation, and are long lasting - just to name a few.

Images and text via

BeerBellyBlunt

All bets are off on what might be the next costume…

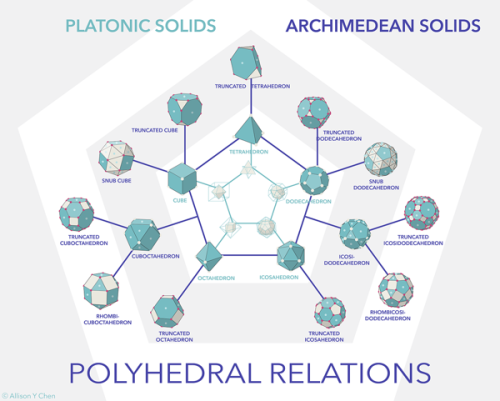
Platonic solid: In Euclidean geometry, a Platonic solid is a regular, convex polyhedron with congruent faces of regular polygons and the same number of faces meeting at each vertex. Five solids meet those criteria, and each is named after its number of faces.

An Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices . They are distinct from the Platonic soilds, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.

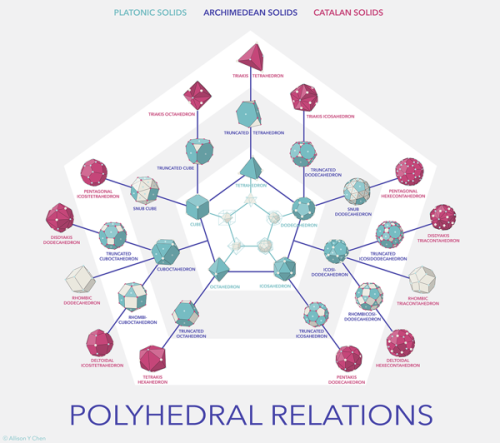
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean soild. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865.

The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic soilds  and Archimedean soild, the faces of Catalan solids are not regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids.

Images: Polyhedral Relations by Allison Chen on Behance.