Sleepysneezeydopeydoc-blog - Physics Nerd

Carrying 69 Chevys…

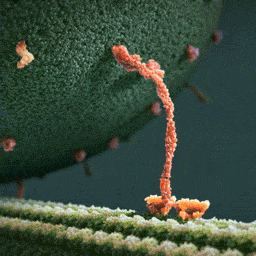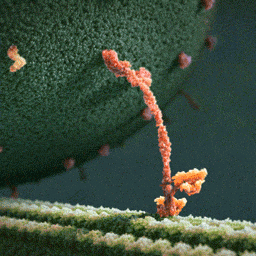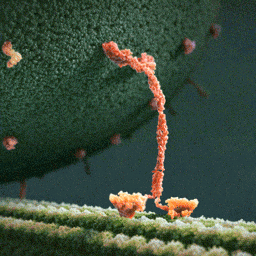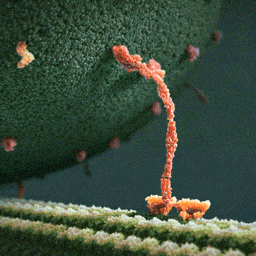
What you see is a myosin protein dragging an endorphin along a filament to the inner part of the brain’s parietal cortex which creates happiness. Happiness. You’re looking at happiness.

1. Take a circle and draw some points on the boundary. For every point you draw, you must also draw its antipode (point on the opposite side of the circle).

2. Draw some points in the interior wherever you want.  3. Label the points either +1, -1, +2, or -2 as you wish. The only stipulation is that antipodes must have opposite sign.

4. Draw triangles however you want without crossing lines.

Tucker’s Lemma says that you will ALWAYS end up with at least one line that has endpoints of either +1 and -1 or +2 and -2. Try it! More info and proof here.

☄️A special relativity problem☄️

This problem appeared in one of my tutorial sheets and I thought it would be a nice one to share.

“A rather eccentric group of astronomy students wanted to celebrate the impact of the Shoemaker-Levy comet on Jupiter by holding a party of sufficiently long duration that their celebrations were simultaneous with the impact of the comet in all inertial frames.

For how long did they need to party?  How might the part end?  [The distance from the Earth to Jupiter is 8 x 10^11 m and you may neglect their relative motion].”

“A time sequence of four frames showing the impact of the first of the 20 odd fragments of Comet Shoemaker-Levy 9 into Jupiter.”

Just basic knowledge of Lorentz transformations is required to solve this 🙂

This question is in fact from Dynamics and Relativity by Gavin Smith and J. R. Forshaw (page 134, problem 6.15). Picture source: NASA.

Higgs Boson

On the 4th of July 2012, ATLAS and CMS experiments both reported a particle with a mass of around 126GeV at CERN’s Large Hadron Collider. The particle is consistent with the Higgs boson predicted by the standard model.

The Higgs boson creates a Higgs field which theoretically exists everywhere in the universe and interacts with subatomic fundamental particles like quarks and leptons to give them mass. How much mass a particle has depends on how much interaction is has with the field, all particles are equal before they enter the Higgs field, it is the Higgs field that gives the particles mass depending on their interactions with it.

In the Standard Model, the higgs field is a scalar tachyonic field ( “scalar” meaning that it doesn’t transform under Lorentz transformations and “tachyonic” referring to the field as a whole having imaginary, or complex, mass). While tachyons are purely theoretical particles that move faster than the speed of light, fields with imaginary mass have an important role in modern physics.

Happy national periodic table day!

On the care and keeping of your scientist

Congratulations on adopting a scientist! Regardless of their field they will require much coffee, free food, and love. Here are some field specific tips for keeping your scientist happy and healthy!

Biology: make sure they don't get overly invested in their model organism by reminding them about the flaws inherent in their system on a regular basis, but also make sure to join in when they criticize other models in favor of their own

Chemistry: don't let them do that 'just one more reaction' at 10 pm. make sure they get out of the lab and see the sun on a regular basis. try to keep them from partying too hard when they do leave the lab

Geology: humor their rock puns but don't let the lick the rocks (they will tell you they need to lick the rocks to identify them, but don't fall for it)

Astronomy: try not to let them become completely nocturnal. point out nice stars to them and look suitably impressed by their "pictures" of planets that don't look like anything to you

Physics: take them to the park on a regular basis to remind them that things larger than subatomic particles exist. bring a frisbee or a ball to play catch with and be impressed by their ability to calculate trajectories

Math: always make sure to have free batteries for their calculators and a mathmatica user guide on hand. Humor them when they tell you why space without angles is important

Ecology: make sure they remember to wear sunscreen and keep an eye on them in the field. Remind them to come inside and analyze their data occasionally

Psychology: don't mention Freud or ever call them a soft or social science, but make sure you gently remind them that social factors can impact reproducibility and try to keep them from drawing sweeping conclusions about the inherent nature of humanity

Neuroscience: be suitably impressed by their newest experiment and then remind them that people are not mice as often as possible

Computer Science: make sure they take breaks while debugging by limiting their supply of coffee. Nod and smile when they go off on indexing and arrays. Make sure they always have a rubber duck.

Make sure to keep your scientist away from engineers unless they have been properly socialized to interact in a translational household. The most important thing is to remember to hug your scientist on a regular basis and remind them that there is life outside the lab

Mathematical Spirals

According to Wikipedia, a spiral is a curve which emanates from a central point, getting progressively farther away as it revolves around the point (similar to helices [plural for helix!] which are three-dimensional). Pictured above are some of the most important spirals of mathematics.

Logarithmic Spiral: Equation: r=ae^bθ. I must admit that these are my favorite! Logarithmic spirals are self-similar, basically meaning that the spiral maintains the same shape even as it grows. There are many examples of approximate logarithmic spirals in nature: the spiral arms of galaxies, the shape of nautilus shells, the approach of an insect to a light source, and more. Additionally, the awesome Mandelbrot set features some logarithmic spirals. Fun fact: the Fibonacci spiral is an approximation of the Golden spiral which is only a special case of the Logarithmic spiral. 

Fermat’s Spiral: Equation: r= ±θ^(½). This is a type of Archimedean spiral and is also known as the parabolic spiral. Fermat’s spiral plays a role in disk phyllotaxis (the arrangement of leaves in a plant system). 

Archimedean Spiral: Equation: r=a+bθ. The Archimedean spiral has the property that the distance between each successive turning of the spiral remains constant. This kind of spiral can have two arms (like in the Fermat’s spiral image), but pictured above is the one-armed version. 

Hyperbolic Spiral: Equation: r=a/θ. It is also know as the reciprocal spiral and is the opposite of an Archimedian spiral. It begins at an infinite distance from the pole in the center (for θ starting from zero r = a/θ starts from infinity), and it winds faster and faster around as it approaches the pole; the distance from any point to the pole, following the curve, is infinite.